Question: A 250-V, 4-pole, wave-wound d.c. series motor has 782 conductors on itsarmature. It has armature and series field resistance of 0.75 ohm. The motor takesa current of 40 A. Estimate its speed and gross torque developed if it has a flux per pole of 25 mWb Answer: Step 1 Mechanical Engineering homework question answer, step 1, image 1 Mechanical Engineering homework question answer, step 1, image 2 Step 2 Mechanical Engineering homework question answer, step 2, image 1 Step 3 Mechanical Engineering homework question answer, step 3, image 1

Link will be apear in 30 seconds.

Well done! you have successfully gained access to Decrypted Link.

https://www.chegg.com/homework-help/questions-and-answers/describe-kepler-s-three-laws-planetary-motion-q41019169

ad

Kepler enunciated the three law of planetary motion after a laborious analysis, extending over long 18 years, of a vast amount of data collected by Tycho Brahe over the years, of the position of the planets, without the use of even any telescope. His three laws of planetary motion are described below.

First law:

All planet move in elliptic orbit round the sun that occupies one of the focus of the ellipse.

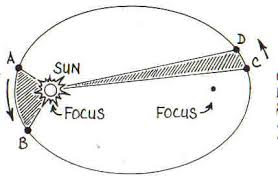
As we can see in the above image that a planet moving around the sun in a elliptic orbit. Now the elliptic orbit means that the path of the planet around the sun is an ellipse. Now we all know from mathematics that ellipse is a curved line forming a closed loop, where the sum of the distances from two points ( called focus of ellipse) to every point on the line is constant. So in the above image the distance from first focus (where the sun is located) to point A plus the distance from the second focus to the point A is always constant. The sun is situated at one of the focus point of the ellipse as in the above image the sun is situated in the left focus point.

Second law:

The radius vector  of the planet from the sun sweeps out equal areas in the equal times.

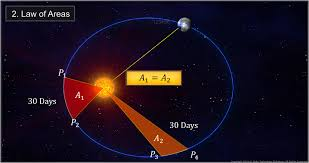
Here we can think radius vector as a straight line connecting sun and the planet. So as the planet moves around the sun, this radius vector that is the straight line, sweeps out some area. Now the speed and the distance of the planet from the sun changes as the planet moves around the sun. But the area swept out by the radius vector ( the line connecting the planet and sun) is equal in equal time interval. In the above image when the planet moves from point  to point  , the area swept out by the radius vector is  and when when the planet moves from point  to point  the area swept out by the radius vector is  . Then according to the second law planetary motion these two area would be same. So according to second law of Kepler planetary motion  .

Third law:

The square of the period of the revolution of the planet is directly proportional to the cube of the semi-major axis of the elliptic orbit.

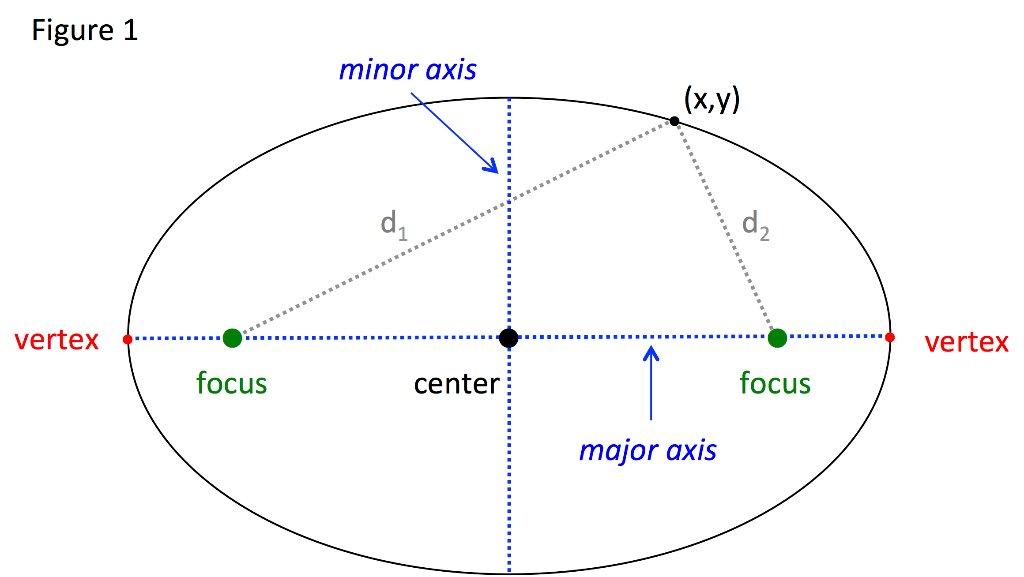
Here the major axis of ellipse is a axis passes through two focuses of the ellipse as shown in the above image. The length of semi-major axis is the distance from the center of the ellipse to the one of vertex. The time of revolution of a planet is the time taken by the planet to complete a full revolution around the sun along the elliptic orbit. Let the time of revolution is T and the length of semi-major axis is a , then according to the third law of planetary motion square T is directly proportional to the cube of a . That is  .