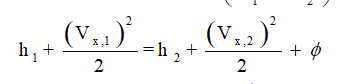The crew survived and wants to study the shock wave in more detail. It can be assumed that the shock wave travels through a stationary flow of an ideal polytropic gas which is adiabatic on both sides of the shock. Properties in front and behind a shock are related through the three Rankine-Hugoniot jump conditions (mass, momentum, energy conservation): P10 = P202 Pv+P1 = px} + P2 where ,,p, and h are the density, shock velocity, pressure, and specific enthalpy in front (1) and behind (2) the shock respectively. Shock front (a) Explain briefly the following terms used in the text above: 0) stationary flow (ii) polytropic gas (ii) specific enthalpy (b) Show with the Rankine-Hugoniot conditions that the change in specific enthalpy is given by: Ah = P2P (+) 2 The general form of Bernoulli's law is fulfilled on both sides of the shock separately: 22 · + +h= b where is the gravitational potential and ba constant. (c) Assuming that the gravitational potential is the same on both sides, determine how the con- stant b changes at the shock front. (d) Explain whether Bernoulli's law can be applied across shock fronts.

Link will be apear in 30 seconds.

Well done! you have successfully gained access to Decrypted Link.

 "

Question:

Problem B.2: Shock Wave 6Points$6Points$
This year’s qualification round featured a spaceship escaping from a shock wave ProblemB$ProblemB$.
The crew survived and wants to study the shock wave in more detail. It can be assumed that
the shock wave travels through a stationary flow of an ideal polytropic gas which is adiabatic on
both sides of the shock. Properties in front and behind a shock are related through the three
Rankine-Hugoniot jump conditions mass,momentum,energyconservation$mass,momentum,energyconservation$:
ρ1v1 = ρ2v2 ρ1v
2
1 + p1 = ρ2v
2
2 + p2
v
2
1
2
+ h1 =
v
2
2
2
+ h2
where ρ, v, p, and h are the density, shock velocity, pressure, and specific enthalpy in front 1$1$
and behind 2$2$ the shock respectively.
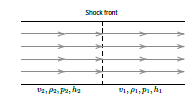
Shock front
v2, ρ2, p2, h2 v1, ρ1, p1, h1
a$a$ Explain briefly the following terms used in the text above:
i$i$ stationary flow
ii$ii$ polytropic gas
iii$iii$ specific enthalpy
b$b$ Show with the Rankine-Hugoniot conditions that the change in specific enthalpy is given by:
∆h =
p2 − p1
2
·
�
1
ρ1
+
1
ρ2
�
The general form of Bernoulli’s law is fulfilled on both sides of the shock separately:
v
2
2
+ Φ + h = b
where Φ is the gravitational potential and b a constant.
c$c$ Assuming that the gravitational potential is the same on both sides, determine how the constant b changes at the shock front.
d$d$ Explain whether Bernoulli’s law can be applied across shock fronts.

---

Answer:

Step 1

Bartleby policy allows me to answers only three question

Ans a

Stationary Flow

A flow in which the velocity of the fluid at a particular fixed point does not change with time means 

 

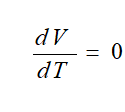
This is known as stationary flow

Polytropic Gas

A gas is called polytropic gas if it obeys the polytropic thermodynamic process means

 

Step 2

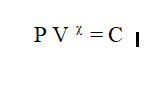
Specific Entropy

It is the total energy in the system due to pressure and temperature per unit of mass in that system.

Application

It is used in thermodynamics equation when one wants to know that energy for a given single unit of mass of the substance

SI unit of specific enthalpy is KJ/Kg.

Ans b

Show with the Rankine-Hugoniot conditions that the change in specific enthalpy is given by:

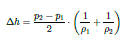
First, Let derive an expression for (Vx,1)2 and (Vx,2)2

where 1 and 2 denote for initial and final states

 

Step 3

Since,

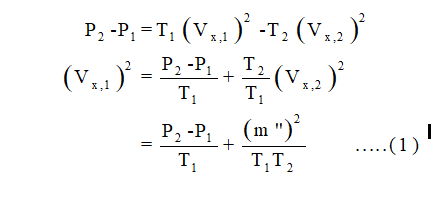
Similarly,

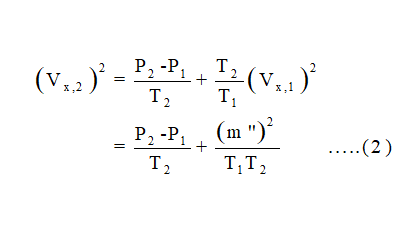
From  1 and 2

Step 4

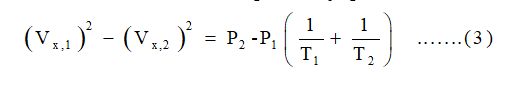
Now, derivation of the Rankin relation energy equation and ideal gas law

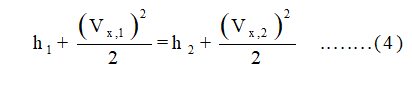
Now, substitute momentum equation 3 into the energy equation 4. we get

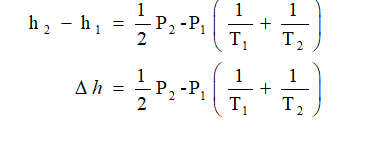
This is the final Rankine-Hugoniot releation

 

Step 5

Ans d

since at shock first, we already see that in the derivation of Rankine equation. That there is conservation of mass, momentum, and energy

Therefore, we derived 4 equations for the momentum equation which is the Bernoulli equation.