QUESTION 6 (a) The bar shown in Figure Q2(a) is subjected to tensile load of 150 Kn. If the stress in the middle portions is limited to 160 N/mm², determine the diameter of the middle portion. Find also the length of the middle portion if the total elongation of the bar is to be 0.25 mm. E E = 2.0 + 105N/mm². (12 marks) 150 KN 10 cm DIA 10 cm DIA 150 KN 45 cm Figure Q6(a) (b) A brass bar, having cross-section area of 900 mm², is subjected to axial forces as shown in Figure Q2(b), in which AB = 0.6 m, BC = 0.8 m, and CD = 1.0 m. Find the total elongation of the bar. E = 1.0 + 105N/mm2 . (8 marks) Page 4 of 5 B D 40 KN 70 KN 20 KN 10 KN Figure Q6(b) (TOTAL = 20 MARKS)

Link will be apear in 30 seconds.

Well done! you have successfully gained access to Decrypted Link.

Textbook Solution:

---

Answer:

To determine

To:

a) find the coordinate asamultipleofdistanceL$asamultipleofdistanceL$ on the x-axis at which the net electric field of particle 1 and particle 2 is zero

b) sketch the net electric field lines between and around the particles.

Answer

Answer:

a) The distance of the point at which net electric field of particle 1 and particle 2 zero is 2.72L$2.72L$

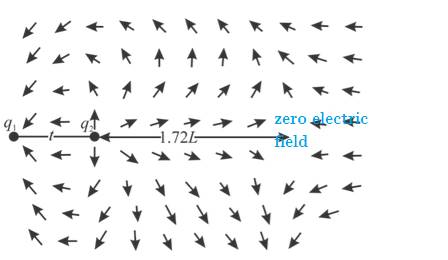
b) Sketch of net electric field lines between and around the two charged particles is

Explanation

1) Concept:

If there are two unlike charges the electric field in between them will be no be xero.

Hence the point at which electric field is zero located either at right or left side depending on magnitude of given charges. That is the point is away from larger charge.

The electric field set up by a positively charged particle always point directly away from the particle. Those set up by a negatively charged particle always point directly toward the particle. If there are two charges, the field lines always originate from the positive charge and end at the negative charge.

2) Formulae:

i. Net electric field= Σ (electric field due to q1 , q2, …qn)$\mathrm{\Sigma } (electric field due to{ q}_{1 }{, q}_2, \dots q_n)$

ii. The magnitude of the electric field set up by a particle with charge q at distance r from the  particle is

E= k qr2$E= k \frac{q}{r^2}$

Where k- 14πεo $\frac{1}{4\pi {\epsilon }_o}$ is the Coulomb’s constant which is equal to 8.99 x 109 N.m2C2$\frac{N.m^2}{C^2}$

3) Given:

Charge on the particle 1, q1$q_1$ = -5.00q

Charge on the particle 2,q2$q_2$ = +2.00q

Distance of separation=L

4) Calculations:

a$a$

Since one charge is positive and another is negative, the net electric field cannot be zero in between them. Assume the point P where the net electric field is zero is to the right of q2 at a distance x from it.

The location of charges and the point are shown in the following figure

Electric field on P due to q1 , E1=k(5q)(L+x)2$, E_1=\frac{k\left(5q\right)}{(L+x{)}^2}$

Electric field on P due to q2 , E2=k(2q)x2$, E_2=\frac{k\left(2q\right)}{x^2}$

For net electric field to be zero on the axis

E1−E2=0$E_1-E_2=0$

k(5q)(L+x)2− k(2q)x2=0$\frac{k\left(5q\right)}{(L+x{)}^2}- \frac{k\left(2q\right)}{x^2}=0$

5x2−2(L+x)2=0$5x^2-2(L+x{)}^2=0$

3x2−4Lx−2L2=0$3x^2-4Lx-2L^2=0$

Solve this quadratic equation using the formula

x=−b±b2−4ac√2a$x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}$

We get

x=1.72L   or   x=0.387L $x=1.72L or x=0.387L$

x=0.387L$x=0.387L$ is not valid as net electric field will not be zero in between the two charges.

Hence, electric field will be zero at a distance 1.72L   $1.72L$ from the second charge.

Therefore from 5q$5q$, the distance will be

d=1.72L+L$d=1.72L+L$

=2.72L$=2.72L$

The distance of the point at which net electric field of particle 1 and particle 2 zero is 2.72L$2.72L$

b$b$

Sketch of net electric field lines between and around the particles

Conclusion

The co-ordinate of point at which net electric field is zero can be found be equating the individual electric fields acting on the point due to given two charges.